Finding Square Roots

| Comments

Most of us has at some point in our lives used the Math.sqrt() function. We would even know that \(\sqrt{2} = 1.414\ldots\). However, we never really give how it is implemented a second thought. Thus is the power of a tight abstraction. For those of us who lived in the age of calculators, finding square roots has always been a source of mystery. For me during my teenage years, calculating a square root has really just been about looking up a numeric table.

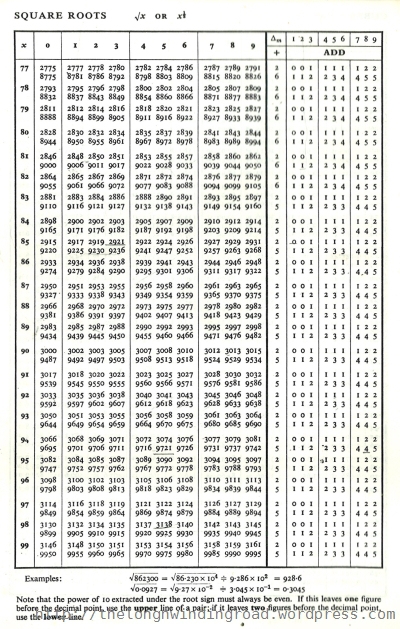
Table of Square Roots

Obviously this very simple problem would have been solved close to the beginnings of civilization, and blazingly fast methods must already exist. But for sake of exploration, let us examine how we would implement a square root function should we need to.

\[\sqrt{-n} = \sqrt{-1} \sqrt{n}\]

Since square roots of negative numbers are really just square roots of positive numbers times the square root of a negative number, let us focus our efforts on finding just the square roots of positive real numbers.

y=x^2

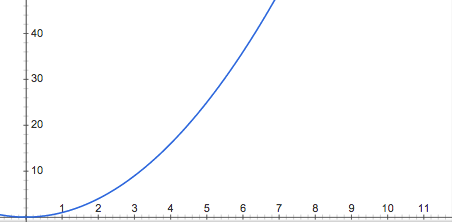
One way to find a square root is by looking at this graph of \(y=x^2\). Simply drawing a horizontal line from the y-axis from whose square root we desire to the graph line, and then find the intersect on the x-axis. So say we want \(\sqrt{30}\).

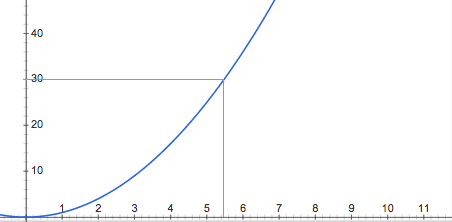
find sqrt 30

We simply draw a line from the y-axis at 30 to the graph and find that it is located somewhere between 5.4 and 5.6 along the x-axis, but closer to 5.4. This makes sense. A quick glance at google) shows \(\sqrt{30} = 5.4772255\)

find sqrt 30

This in-betweenness tells us something about square roots. Besides the nice square roots, the ugly ones don’t seem to have any end to their decimals. Hence, they are always in between two numbers that we know. This means that we can keep making educated guesses about where the square root is until we get close enough.

\[0 < \sqrt{30} < 30\]

Let’s apply this knowledge first and do the calculation by hand for the number 30 since we know its answer so we can verify that our method is correct.

First of all, we must figure out where the root is. Obviously, it would be less than 30, since you need to multiply it by itself to get 30. Its also more than zero, because as mentioned earlier, you will always end up with a positive number.

\[\sqrt{30} \approx 15?\]

The number most in between of 0 and 30 is 15. But is this the number? The only way to check is by squaring 15.

\[15^2 = 225\]

Nope. Not even close. 225 is waaay too big. But this tells us something: the root cannot be bigger than 15 because if it was, we would get an even bigger square than 30, so we must look to the left of 15. This means our upper bound is now 15 instead of 30.

\[0 < \sqrt{30} < 15\]

The number in the middle this time is 7.5. Is this our number?

\[7.5^2 = 56.25\]

Still too big. This means our root must be smaller than 7.5, but still bigger than zero.

\[0 < \sqrt{30} < 7.5\]

The number in the middle of 7.5 is 3.75. Perhaps this is our number?

\[3.75^2 = 14.0625\]

It seems the square of 3.75 is smaller than 30! This means that that the root must be bigger than 3.75 since if the number is smaller, we get an even smaller square, we must be getting close.

\[3.75 < \sqrt{30} < 7.5\]

Now we must find out what number is in the middle. Well, from our geometry class we know that the average of two numbers is the middle number, so \(\frac{3.75 + 7.5}{2} = 5.625\). We simply need to square this number to check now.

\[5.625^2 = 31.640625\]

It seems we have gotten a lot closer now that we moved the lower bound up. Our guess of 5.625 seems really close to the answer now. But because its square is bigger than 30, we know the root must be smaller than 5.625, so:

\[3.75 < \sqrt{30} < 5.625\]

The middle number of this is then 4.6875.

\[4.6875^2 = 21.972656\]

That’s really far away. This can’t be the answer, but lets keep looking. Since its square is smaller than 30, we change the lower bound to this.

\[4.6875 < \sqrt{30} < 5.625\]

This time, the middle number is 5.15625.

\[5.15625^2 = 26.586914\]

We are getting closer again, but this is smaller than 30, so our lower bound should be changed.

\[5.15625 < \sqrt{30} < 5.625\]

I know, it starts to get frustrating at this point since we seem to be crawling, but lets stay on for another two rounds. The number in the middle is 5.390625

\[5.390625^2 = 29.058838\]

Our result now is very very close to 30. It is smaller, so the lower bound should be changed.

\[5.390625 < \sqrt{30} < 5.625\]

The middle number is now 5.507812. That means the square is…

\[5.507812^2 = 30.336\]

Okay! We are pretty close, but the important thing is we know it will eventually arrive at the answer because we kept getting closer to the answer as we went. Now, we know computers do things faster than we do so let us write some code!

So first of all, we want to have our initial guess. The number to be rooted is 30.

1
2
3
4

double number = 30;

double upperBound = number;
double lowerBound = 0;

Then, we write down what we did in every iteration.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

// We try and figure out if the middle number is the correct root
double rootGuess = (upperBound + lowerBound) / 2;
double rootGuessSquared = rootGuess * rootGuess;

if (rootGuessSquared > number)
{
  // if the square of our guess is bigger than the number, that means the root is too big.
  // so the root cannot be bigger than our current guess
  upperBound = rootGuess;
}
else
{
  // otherwise, the root cannot be smaller than our current guess.
  lowerBound = rootGuess;
}

Next, we tell the computer to do it over and over again until the square of our guess is the number itself, so we wrap that in a loop.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

double rootGuess = 0;
do
{
  // We try and figure out if the middle number is the correct root
  rootGuess = (upperBound + lowerBound) / 2;
  double rootGuessSquared = rootGuess * rootGuess;

  if (rootGuessSquared > number)
  {
      // if the square of our guess is bigger than the number, that means the root is too big.
      // so the root cannot be bigger than our current guess
      upperBound = rootGuess;
  }
  else
  {
      // otherwise, the root cannot be smaller than our current guess.
      lowerBound = rootGuess;
  }

} while(rootGuess * rootGuess != number);

Great, that seems simple enough. Let’s put it all together.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

double number = 30;

double upperBound = number;
double lowerBound = 0;

double rootGuess = 0;
do
{
  // We try and figure out if the middle number is the correct root
  rootGuess = (upperBound + lowerBound) / 2;
  double rootGuessSquared = rootGuess * rootGuess;

  if (rootGuessSquared > number)
  {
      // if the square of our guess is bigger than the number, that means the root is too big.
      // so the root cannot be bigger than our current guess
      upperBound = rootGuess;
  }
  else
  {
      // otherwise, the root cannot be smaller than our current guess.
      lowerBound = rootGuess;
  }

  printf("%lf < sqrt(30) < %lf guess=%lf rootGuessSquared=%lf\n", upperBound, lowerBound, rootGuess, rootGuessSquared);

} while(rootGuess * rootGuess != number);

printf("result = %lf\n", rootGuess);

Notice I put in a printf to check the bounds as it runs. This makes it more interesting and actually shows us what’s going on. Lets run it now.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

15.000000 < sqrt(30) < 0.000000 guess=15.000000 rootGuessSquared=225.000000
7.500000 < sqrt(30) < 0.000000 guess=7.500000 rootGuessSquared=56.250000
7.500000 < sqrt(30) < 3.750000 guess=3.750000 rootGuessSquared=14.062500
5.625000 < sqrt(30) < 3.750000 guess=5.625000 rootGuessSquared=31.640625
5.625000 < sqrt(30) < 4.687500 guess=4.687500 rootGuessSquared=21.972656
5.625000 < sqrt(30) < 5.156250 guess=5.156250 rootGuessSquared=26.586914
5.625000 < sqrt(30) < 5.390625 guess=5.390625 rootGuessSquared=29.058838
5.507812 < sqrt(30) < 5.390625 guess=5.507812 rootGuessSquared=30.335999
5.507812 < sqrt(30) < 5.449219 guess=5.449219 rootGuessSquared=29.693985
5.478516 < sqrt(30) < 5.449219 guess=5.478516 rootGuessSquared=30.014133
5.478516 < sqrt(30) < 5.463867 guess=5.463867 rootGuessSquared=29.853845
5.478516 < sqrt(30) < 5.471191 guess=5.471191 rootGuessSquared=29.933935
5.478516 < sqrt(30) < 5.474854 guess=5.474854 rootGuessSquared=29.974021
5.478516 < sqrt(30) < 5.476685 guess=5.476685 rootGuessSquared=29.994074
5.477600 < sqrt(30) < 5.476685 guess=5.477600 rootGuessSquared=30.004103
5.477600 < sqrt(30) < 5.477142 guess=5.477142 rootGuessSquared=29.999088
5.477371 < sqrt(30) < 5.477142 guess=5.477371 rootGuessSquared=30.001595
5.477257 < sqrt(30) < 5.477142 guess=5.477257 rootGuessSquared=30.000342
5.477257 < sqrt(30) < 5.477200 guess=5.477200 rootGuessSquared=29.999715
5.477228 < sqrt(30) < 5.477200 guess=5.477228 rootGuessSquared=30.000028
5.477228 < sqrt(30) < 5.477214 guess=5.477214 rootGuessSquared=29.999872
5.477228 < sqrt(30) < 5.477221 guess=5.477221 rootGuessSquared=29.999950
5.477228 < sqrt(30) < 5.477225 guess=5.477225 rootGuessSquared=29.999989
5.477226 < sqrt(30) < 5.477225 guess=5.477226 rootGuessSquared=30.000009
5.477226 < sqrt(30) < 5.477225 guess=5.477225 rootGuessSquared=29.999999
5.477226 < sqrt(30) < 5.477225 guess=5.477226 rootGuessSquared=30.000004
5.477226 < sqrt(30) < 5.477225 guess=5.477226 rootGuessSquared=30.000001
5.477226 < sqrt(30) < 5.477225 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
5.477226 < sqrt(30) < 5.477226 guess=5.477226 rootGuessSquared=30.000000
result = 5.477226

After all that spam, now we can see that the result is the square root of 30, since we know 5.477226 is the square root of 30.

This method of calculating square roots is called the Bisection method, also known as a binary search. Its not very efficient as you can see, and takes a long time to converge.

Now we know what it takes to find a square root! Now you can simply try it with a bunch of numbers and get the right answer. You can also compare the answer with the actual sqrt() function provided by the standard library.

It is also interesting to note that you can use this method to get cube roots, quartic roots and quintic roots too.

Comments